模擬授業「“理想数” をめぐる冒険」（8月14日）を開催します

2022年8月14日 (日) に行われるオープンキャンパス内において、模擬授業を開催します。参加方法については、オープンキャンパス特設サイト（下記リンク）を参照ください。

時間：
9:30 〜 10:20

場所：
5号館5101教室（定員133名）

講師：
原隆准教授

講義名：
“理想数” をめぐる冒険－－数の分解の一意性を追い求めて

講義内容：

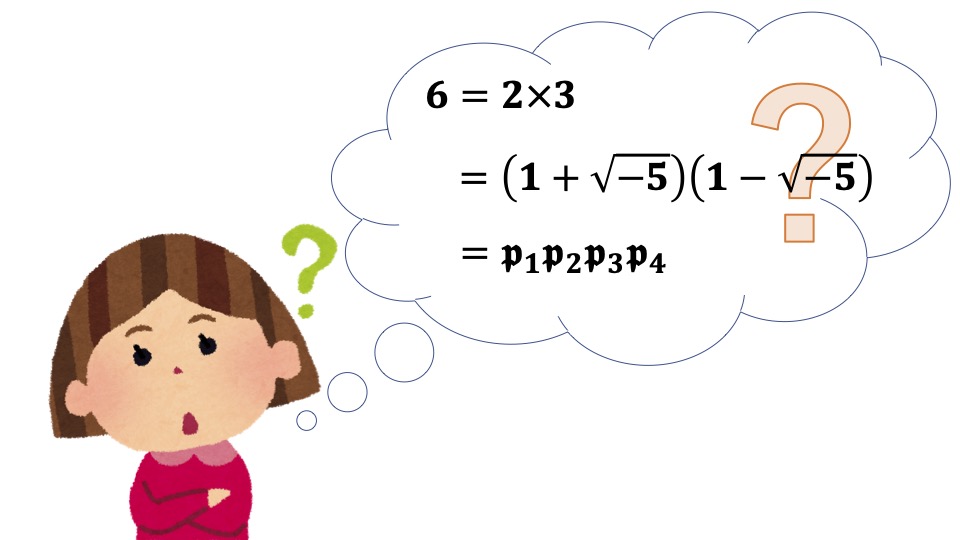
皆さんは、誰もが1度くらいは整数の素因数分解を計算した経験があることでしょう。たとえば12は12=2×2×3と「2が2つと3が1つの積」に分解されますが、いつ、どこで、誰が素因数分解をしても、その結果は同じであること－－地球の裏側のブラジルで素因数分解しても、あるいは紀元前の古代ギリシアで素因数分解しても12はいつだって「2が2つと3が1つの積」であること－－を、皆さんは「当たり前のこと」として、これまで何の疑問も抱いてこなかったと思います。

それでは、整数だけでなく「2乗すると -5 になる数 √(-5)」も使って良いことにするとどうなるでしょうか？すると、例えば6という数は6=2×3=(1+√(-5))(1-√(-5)) と “2通りの分解” を持ちますが、ここに出てきた2, 3, 1+√(-5), 1-√(-5) はどれもこれ以上分解できない数 (“素数”) なのです‼このように、ちょっと数の世界を拡げてみただけで、「素因数分解の結果はいつでも同じ」という皆さんの「常識」はたちまち崩れ去ってしまいます。そんな〈異常事態〉を乗り越えるために、ドイツの数学者エルンスト・クンマーは “理想数” と呼ばれる「数ならぬ数」の概念を考案しました。

フェルマーの最終定理にも関係するこの奇妙な数 “理想数” とは、一体何者なのでしょうか？－－この公開授業では、誰もが知っている素因数分解の話から出発して、皆さんの「常識」が通用しないミステリアスな数の世界を、一緒に探検していくことにしましょう。